Due: Before class, September 24th, 2024.

A major theme of Tuesday's lecture, and a major theme of our class, is how poor sampling and reconstruction can lead to aliasing.

Aliasing means, roughly speaking, when something appears to be what it is not. (In English, an "alias" essentially just means a false name or identity.) In computer graphics and signal processing, aliasing occurs because of a mismatch between sampling and reconstruction: the rate or manner in which a signal is sampled is insufficient to provide a faithful reconstruction of the original signal.

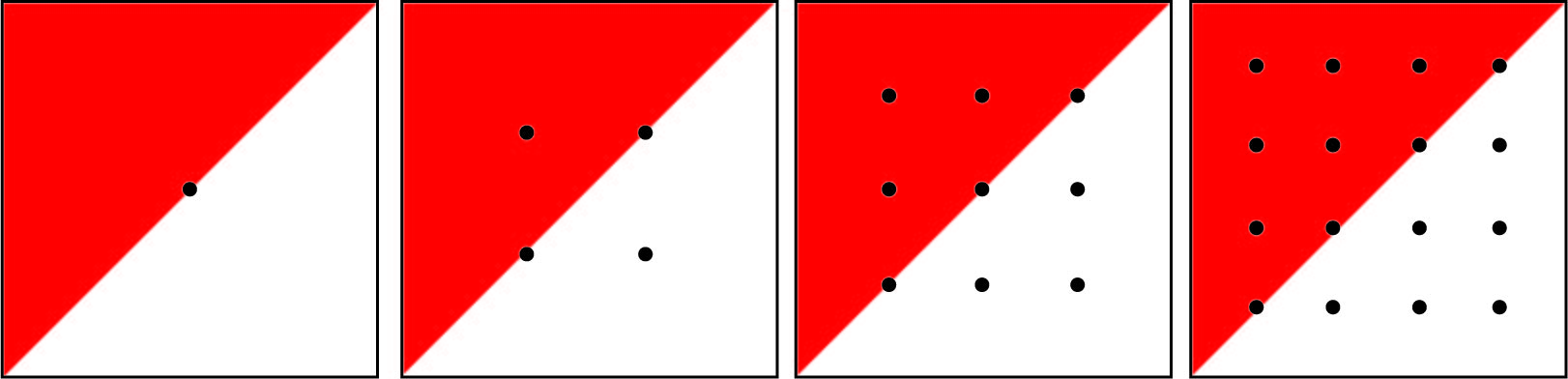
For this exercise we will be looking at how various sampling methods and resolutions can affect the reconstruction of the image. We will be using supersampling to compute the value of the same pixel. For each cell, the red triangle takes up exactly half of the pixel. If the sample is being taken at the edge of the triangle, it is counted as being inside the triangle in this example.

1) What is the percent red for each supersampled pixel? Please compute this for each of the 4 images below.

2) Plot a graph of the relative sampling error as we increase the supersample rate from 1 to 4. Recall that the relative error is abs(samplePercent - truePercent) / truePercent.

3) Based on your graph, what do you notice about the error? Does it increase or decrease in this case? What does that tell you about the pixel accuracy as we increase the supersample rate?

Tuesday's lecture discusses how increasing the sample count can help us more accurately rasterize triangles, but that is not always the case. Consider the following 4x4 supersampling pattern for a single pixel.

4) Draw a set of primitives inside the pixel that would lead to a high relative sampling error.

As you may have noticed, sampling is a difficult problem. We cannot generalize sampling to say that "taking more samples will reduce relative sampling error" since it highly depends on the primitive layout in each pixel. Here's some additional food for thoughts: how do we determine how good a set of sample points is?

5) In the end, go to your favorite resource, for example, the internet, find 2 different anit-aliasing method in computer graphics and briefly describe them.